Problem 1 (教材习题 6-1)

（用插入的方法建堆） 我们可以通过反复调用 MAX-HEAP-INSERT （详见第5讲PPT第43页）实现向一个堆中插入元素，考虑 BUILD-MAX-HEAP 的如下实现方式：

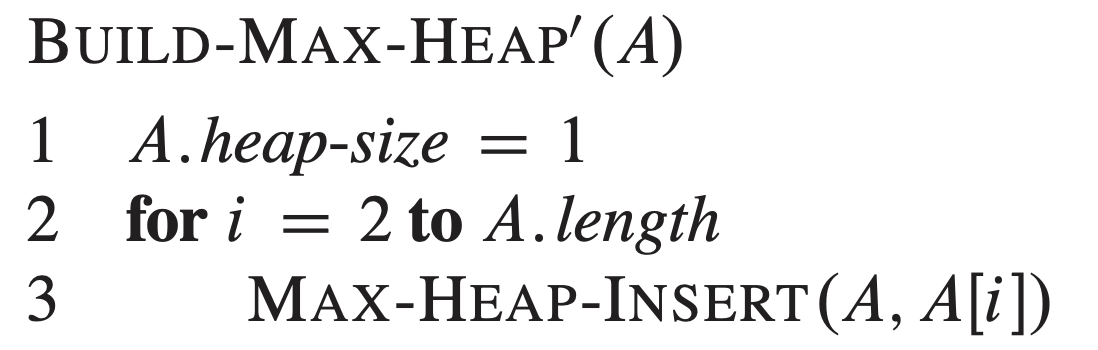
1. 当输入数据相同的时候，BUILD-MAX-HEAP 和 BUILD-MAX-HEAP’ 生成的堆是否总是一样的？如果是，请证明；否则，请举出一个反例。

2. 证明：在最坏情况下，调用 BUILD-MAX-HEAP’ 建立一个包含 $n$ 个元素的堆的时间复杂度是 $\Theta(n\log n)$ 。

Solution

1. 不总是一样的，考虑反例 $A = \langle 1, 2, 3\rangle$ ：

   • 调用 BUILD-MAX-HEAP 后得到 $A = \langle 3, 2, 1 \rangle$ ；

   • 调用 BUILD-MAX-HEAP’ 后得到 $A = \langle 3, 1, 2 \rangle$ 。

2. 证明：最坏情况下 MAX-HEAP-INSERT 的时间复杂度为 $\Theta(n\log n)$ ，而 BUILD-MAX-HEAP’ 算法第 2 到 3 行的 for 循环调用了 $k - 1$ 次 MAX-HEAP-INSERT ，因此 BUILD-MAX-HEAP’ 最坏情况下的时间复杂度为 $\Theta(n\log n)$ 。

BUILD-MAX-HEAP 的复杂度只有 $O(n)$ （见第5讲PPT第19页），所以逐个插入并不是一种高效的建堆方法。

Problem 2 (教材习题 6-2)

（对 d 叉堆的分析） $d$ 叉堆与二叉堆很类似，但其中的每个非叶结点有 $d$ 个孩子，而不是仅仅 2 个。

1. 如何在一个数组中表示一个 $d$ 叉堆？

2. 包含 $n$ 个元素的 $d$ 叉堆的高度是多少？请用 $n$ 和 $d$ 表示。

3. 请给出 EXTRACT-MAX 在 $d$ 叉最大堆上的一个有效实现，并用 $d$ 和 $n$ 表示出它的时间复杂度。

4. 给出 INSERT 在 $d$ 叉最大堆上的一个有效实现，并用 $d$ 和 $n$ 表示出它的时间复杂度。

5. 给出 INCREASE-KEY(A, i, k) 的一个有效实现。当 $k < A[i]$ 时，它会触发一个错误，否则执行 $A[i] = k$ ，并更新相应的 $d$ 叉最大堆。请用 $d$ 和 $n$ 表示出它的时间复杂度。

Solution

1. 我们只需要给出对于下标为 $i$ 的结点计算其父子结点下标的算法即可。

其中，$1 \le k \le d$ ，我们可以很容易地验证：

$\begin{aligned}$
\text{D-PARENT}(\text{D-CHILD}(i, k)) &= \lfloor (\text{D-CHILD}(i, k) - 2) / d + 1\rfloor\
&= \lfloor ((d * (i - 1) + k + 1) - 2) / d + 1\rfloor\
&= \lfloor i + (k - 1) / d \rfloor\
&= i + \lfloor (k - 1) / d \rfloor\
&= i
\end{aligned}

2. 由于每个结点都有 $d$ 个子结点，$n$ 个结点的 $d$ 叉堆的高度为 $\Theta(\log_b n)$ 。

3. 思路和二叉堆一样，唯一的区别在于 MAX-HEAPIFY 操作中，每次 $A[i]$ 的下降，二叉堆只需要比较两次就可以了，而 $d$ 叉堆需要比较 $d$ 次。又因为最多需要下降的次数为堆的高度，即 $\Theta(\log_b n)$ ，所以整体的复杂度为 $O(d\log_d n)$ 。

4. 我们将第 4 问和第 5 问放在一起讨论，和二叉堆类似的，算法的复杂度取决于待修改的元素需要“上浮”的次数，不难得出最坏情况下的运行时间为 $O(\log n)$ 。

5. 见第 4 问。

Problem 3 (教材习题 6-3)

（Young 氏矩阵） 在一个 $m\times n$ 的 Young氏矩阵（Young tableau）中，每一行的数据都是从左到右排序的，每一列的数据都是从上到下排序的。Young 氏矩阵中也会存在一些值为 $\infty$ 的数据项，表示那些不存在的元素。因此， Young 氏矩阵可以用来存储 $r \le mn$ 个有限的数。

1. 画出一个包含元素为 ${9, 16, 3, 2, 4, 8, 5, 14, 12}$ 的 $4\times 4$ Young 氏矩阵。

2. 对于一个 $m\times n$ 的 Young 氏矩阵 $Y$ 来说，请证明：如果 $Y[1, 1] = \infty$ ，则 $Y$ 为空；如果 $Y[m, n] < \infty$ ，则 $Y$ 为满（即包含 $mn$ 个元素）。

3. 请给出一个在 $m\times n$ Young氏矩阵上时间复杂度为 $O(m + n)$ 的 EXTRACT-MIN 的算法实现。你的算法可以考虑使用一个递归过程，它可以把一个规模为 $m \times n$ 的问题分解为规模为 $(m - 1)\times n$ 或者 $m \times (n - 1)$ 的子问题（提示：考虑使用 MAX-HEAPIFY）。这里，定义 $T(p)$ 用来表示 EXTRACT-MIN 在任一 $m \times n$ 的 Young 氏矩阵上的时间复杂度，其中 $p = m + n$ 。给出求解 $T(p)$ 的递归表达式，其结果为 $O(m+n)$ 。

4. 试说明如何在 $O(m + n)$ 的时间内，将一个新元素插入到一个未满的 $m \times n$ 的 Young 氏矩阵中。

5. 在不用其他排序算法的情况下，试说明如何利用一个 $n \times n$ 的 Young 氏矩阵在 $O(n^3)$ 时间内将 $n^2$ 个数进行排序。

6. 设计一个时间复杂度为 $O(m + n)$ 的算法，它可以用来判断一个给定的数是否存储在 $m \times n$ 的 Young 氏矩阵中。

Solution

1. 答案不唯一，下面给出两个例子。

$\left[$
\begin{matrix}
2 & 3 & 4 & 5\
8 & 9 & 12 & 14\
16 & \infty & \infty & \infty\
\infty & \infty & \infty & \infty\
\end{matrix}
\right],
\left[
\begin{matrix}
2 & 3 & 12 & 14\
4 & 8 & 16 & \infty\
5 & 9 & \infty & \infty\
\infty & \infty & \infty & \infty\
\end{matrix}
\right],
\cdots

2. 反证法。

   • 若 $Y[1, 1] = \infty$ ，假设 $Y$ 不为空，则存在 $Y[i, j] = k$ ，其中 $i > 1 \vee j > 1$ ，而 $k < \infty$ ，于是存在逆序对 $(1, i)$ 或者 $(1, j)$ ，与 Young 氏矩阵行列都是排好序的矛盾。因此 $Y$ 为空。

   • 若 $Y[m, n] = k < \infty$ ，假设 $Y$ 不满，则存在 $Y[i, j] = \infty$ ，其中 $i < m \vee j < n$ ，于是存在逆序对 $(i, m)$ 或者 $(j, n)$ ，与 Young 氏矩阵行列都是排好序的矛盾。因此 $Y$ 为满。

3. $Y[1,1]$ 是最小的元素，取出它就可以了，只不过，取出了 $Y[1,1]$ 之后，Young 氏性质就被破坏了，我们需要进行一个类似于 MIN-HEAPIFY 的操作来维护 Young 氏性质。

其中，$Y.\text{row-num}$ 和 $Y.\text{col-num}$ 分别表示 Young 氏矩阵的行数 $m$ 和列数 $n$ 。

过程 YOUNG-EXTRACT-MIN 的复杂度由过程 MATRIX-YOUNIFY 决定，递归式为

$T(p) \le T(p - 1) + O(1)$

不难解得 $T(p) = O(p) = O(m + n)$ 。

4. 本题和上一题是类似的，只不过上一题是从左上角向右下角更新，这一题是从右下角向左上角更新，复杂度依旧是 $O(m + n)$ 。

为了和本讲内容配合，上面两题中，我将算法都分成了两个过程来表述，不过这不是必要的，只是为了展示想法之间的相似性。

5. 基于上面两题，本题的思路是：先调用 YOUNG-INSERT 将 $n^2$ 个元素放入 Young 氏矩阵，再调用 YOUNG-EXTRACT-MIN 将这 $n^2$ 元素取出来，取出的元素顺序就是排好序的元素顺序。

其中，调用 YOUNG-INSERT 和 YOUNG-EXTRACT-MIN 的复杂度为 $O(n + n) = O(n)$ ，各调用了 $n^2$ 次，因此总复杂度为 $O(n^3)$ 。

6. 本题的思路是从矩阵左下角开始，将当前元素 $current$ 和待查询的 $key$ 进行比较：如果 $current > key$ 则继续查询上方的元素；如果 $current < key$ 则继续查询右方元素； 如果 $current = key$ 或者已经查询到了最右上角，则终止算法，返回结果。

不难看出，算法的复杂度为 $O(m + n)$ 。

其实这个算法的思路和练习1-2问题4是类似的，正确性的证明（循环不变式）也是类似的，第 3 到 11 行 while 循环的不变式为：

• 每次循环开始前， $key$ 只有可能存在于子矩阵 $Y[1..i,j..n]$ 中。

熊桑不可能每个算法都给出严格的正确性证明的，那就太冗余了，这个不变式以及这个算法的正确性就留待读者自己思考啦。