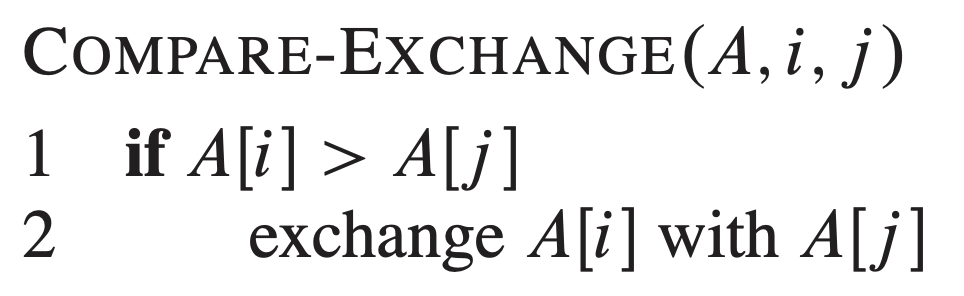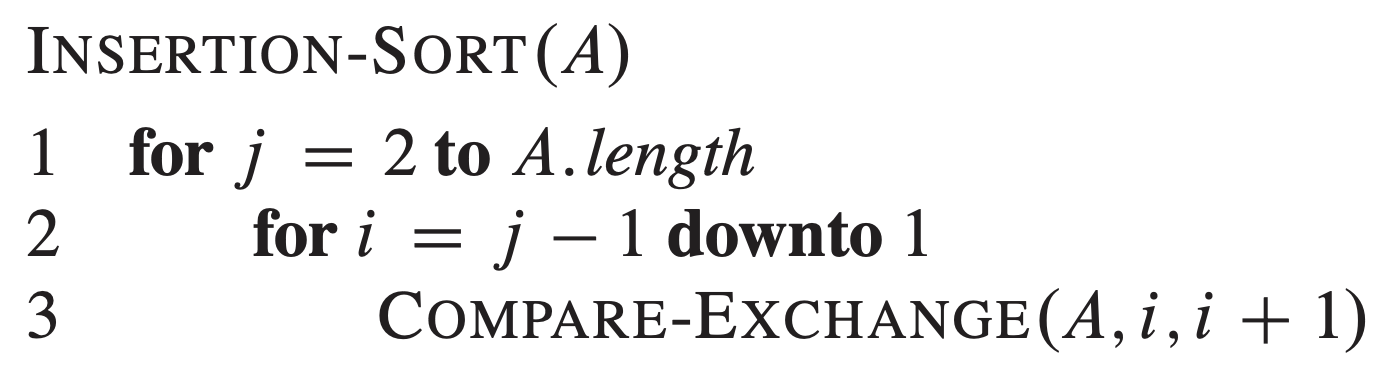Problem 1 (教材习题 8-5)

（平均排序） 假设我们不是要完全排序一个数组，而只是要求数组中的元素在平均情况下是升序的。更准确地说，如果对所有的 $i = 1, 2, \cdots, n-k$ 有下式成立，我们就称一个包含 $n$ 个元素的数组 $A$ 为 k-排序的 （k-sorted）：

$\frac{\sum\limits_{j=i}^{i+k-1}A[j]}{k} \le \frac{\sum\limits_{j=i+1}^{i+k}A[j]}{k}$

1. 一个数组是 $1$ 排序的，表示什么含义？

2. 给出对数字 $1, 2, \cdots, 10$ 的一个排列，它是 $2$ 排序的，但不是完全有序的。

3. 证明：一个包含 $n$ 个元素的数组是 $k$ 排序的，当且仅当对所有的 $i = 1, 2, \cdots ,n - k$ ，有 $A[i] \le A[i+k]$ 。

4. 设计一个算法，它能在 $O(n\log(n/k))$ 时间内对一个包含 $n$ 个元素的数组进行 k 排序。

当 $k$ 是一个常数时，也可以给出 $k$ 排序算法的下界。

5. 证明：我们可以在 $O(n\log k)$ 时间内对一个长度为 $n$ 的 $k$ 排序数组进行全排序。（提示：可以利用练习5-2问题6的结果。）

6. 证明：当 $k$ 是一个常数时，对包含 $n$ 个元素的数组进行 $k$ 排序需要 $\Omega(n \log n)$ 的时间。（提示：可以利用前面解决比较排序的下界的方法。）

Solution

1. 一个数组是 $1$ 排序的，相当于这个数组是从小到大排好序的。

2. $\langle 2,1,4,3,6,5,8,7,10,9\rangle$ 是 $2$ 排序的，但不是完全有序的。

3. 一个包含 $n$ 个元素的数组是 $k$ 排序的，当且仅当对所有的 $i = 1, 2, \cdots ,n - k$ ，有

$\frac{\sum\limits_{j=i}^{i+k-1}A[j]}{k} \le \frac{\sum\limits_{j=i+1}^{i+k}A[j]}{k}$

$\Leftrightarrow \sum_{j=i}^{i+k-1}A[j] \le \sum_{j=i+1}^{i+k}A[j]$

$\Leftrightarrow A[i] + \sum_{j=i+1}^{i+k-1}A[j] \le \sum_{j=i+1}^{i+k-1}A[j] + A[i+k]$

$\Leftrightarrow A[i] \le A[i+k]$

4. 给出两种可行的算法：

   • 算法1： $A[i] \le A[i+k]$ 意味着每一个下标模 $k$ 同余的子数组都是有序的，我们可以将一个长度为 $n$ 的数组按照下标模 $k$ 同余的标准视为 $k$ 个长度为 $n/k$ 的子数组，对每个子数组执行复杂度为 $O((n/k)\log(n/k))$ 的比较排序（归并排序、堆排序、快速排序皆可），排序 $k$ 个子数组的总复杂度为 $k\cdot O((n/k)\log(n/k)) = O(n\log(n/k))$ 。这种排序思路类似于希尔排序（shell sort）。

   • 算法2：使用练习6问题4题干中的算法，我们可以在 $O(n\log(n/k))$ 的时间内将长度为 $n$ 的数组划分为 $n/k$ 个长度为 $k$ 的子数组，其中子数组之间已经排好序，子数组内部不一定排好序。不过长度为 $k$ 的子数组之间排好序就已经满足了 $A[i] \le A[i+k]$ 的要求了。

5. 长度为 $n$ 的 $k$ 排序数组可以按照下标模 $k$ 的结果是为 $k$ 个排好序的子数组，总元素为 $n$。练习5-2问题6给出了一个可以在 $O(n\log k)$ 时间内合并一共有 $n$ 个元素的 $k$ 个有序列表的算法。我们只需要调用该算法即可对一个长度为 $n$ 的 $k$ 排序数组进行全排序。

6. 根据第 3 问结论， $k$ 排序相当于对于每一个同余子数组分别排序。

   • 排序一个长度为 $n / k$ 的子数组的比较次数下界为 $\Omega((n/k)\log(n/k))$ ，排序 $k$ 个这样的子数组的比较次数的下界则为 $k \Omega((n/k)\log(n/k)) = \Omega(n\log(n/k))$ 。

   • 又因为 $k$ 是一个常数，所以 $\Omega(n\log(n/k)) = \Omega(n\log n)$ 。

Problem 2 (教材习题 8-6)

（合并有序列表的下界） 合并两个有序列表是我们经常会遇到的问题。作为 MERGE-SORT 的一个子过程，我们在第1讲PPT第32页已经遇到过这一问题。对这一问题，我们将证明在最坏情况下，合并两个都包含 $n$ 个元素的有序列表所需的比较次数的下界是 $2n-1$ 。

首先，利用决策树来说明比较次数有一个下界 $2n-o(n)$ 。

1. 给定 $2n$ 个数，请算出共有多少种可能的方式将它们划分成两个有序的列表，其中每个列表都包含 $n$ 个数。

2. 利用决策树和第 1 问的答案，证明：任何能够正确合并两个有序列表的算法都至少要进行 $2n-o(n)$ 次比较。

现在我们来给出一个更紧确的界 $2n-1$ 。

3. 请说明：如果两个元素在有序序列中是连续的，且它们分别来自不同的列表，则它们必须进行比较。

4. 利用你对上一部分的回答，说明合并两个有序列表时的比较次数下界为 $2n-1$ 。

Solution

1. 根据分步计数原理，有 $C_{2n}^{n} \times 1 \times 1 = C_{2n}^{n}$ 种方式将它们划分成两个有序列表。

2. 由于 $\log k$ 是一个单调增函数，则有积分放缩式

$\int_{0}^{n}\log x \text{d}x \le \sum_{k=1}^{n} \log k \le \int_{1}^{n+1}\log x \text{d}x$

即

$\frac{n\ln n - n}{\ln 2} \le \sum_{k=1}^{n} \log k \le \frac{(n+1)\ln(n+1) - n}{\ln 2}$

根据第 1 问结果，决策树至少需要有 $C_{2n}^{n}$ 个可达的叶结点，假设决策树高度为 $h$ ，则 $C_{2n}^{n} \le 2^h$ ，即

$\begin{aligned}$
h\ge \log\frac{(2n)!}{(n!)^2}
&= \log((2n)!) - 2 \log(n!)\
&= \sum_{k=1}^{2n}\log(k) - 2\sum_{k=1}^{n}\log(k)\
&\ge \frac{2n\ln(2n)-2n}{\ln 2} - 2\frac{(n+1)\ln(n+1) - n}{\ln 2}\
&=2n + 2n\log n - 2n\log(n+1) - 2\log(n+1)\
&=2n + 2n\log\frac{n}{n+1} - 2\log(n+1)\
&=2n - o(n)
\end{aligned}

因此至少要进行 $2n - o(n)$ 次比较。

3. 由于这两个在有序序列中连续的元素来自不同的列表，它们的顺序在输入序列中是看不出来的，但输出序列中又必须知道这两者的顺序，因此，它们必须进行比较。

4. 考虑 $A = \langle 1, 3, 5, \cdots, 2n-1\rangle$ ， $B = \langle 2， 4， 6，\cdots, 2n\rangle$ 。根据第 3 问，我们必须比较 $1$ 和 $2$ ， $2$ 和 $3$ ， $3$ 和 $4$ ，一直到 $2n-1$ 和 $n$ ，一共 $2n-1$ 次比较。因此比较次数的下界最多为 $2n-1$ ，又因为下界至少为 $2n-o(n)$ ，因此下界的紧确界就是 $2n-1$ 。

Problem 3 (教材习题 8-7)

（0-1 排序引理和列排序） 针对两个数组元素 $A[i]$ 和 $A[j]$ （ $i < j$ ）的 比较交换 操作的形式如下：

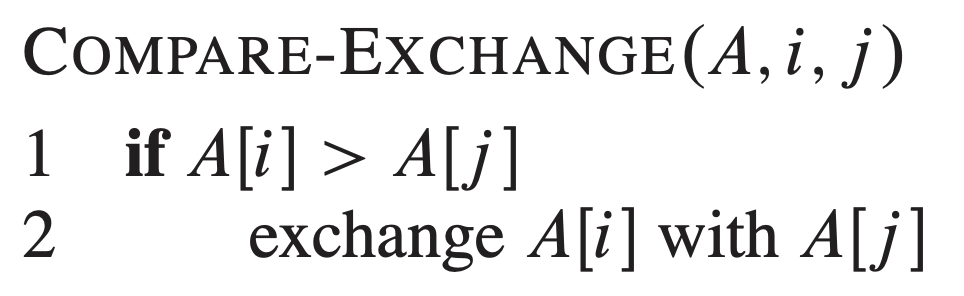
经过比较交换操作之后，我们得到 $A[i] \le A[j]$ 。

遗忘比较交换算法 是指算法只按照事先定义好的操作执行，即需要比较的位置下标必须事先确定好。虽然算法可能依靠待排序元素个数，但它不能依赖待排序元素的值，也不能依赖任何之前的比较交换操作的结果。例如，下面是一个基于遗忘比较交换算法的插入排序：

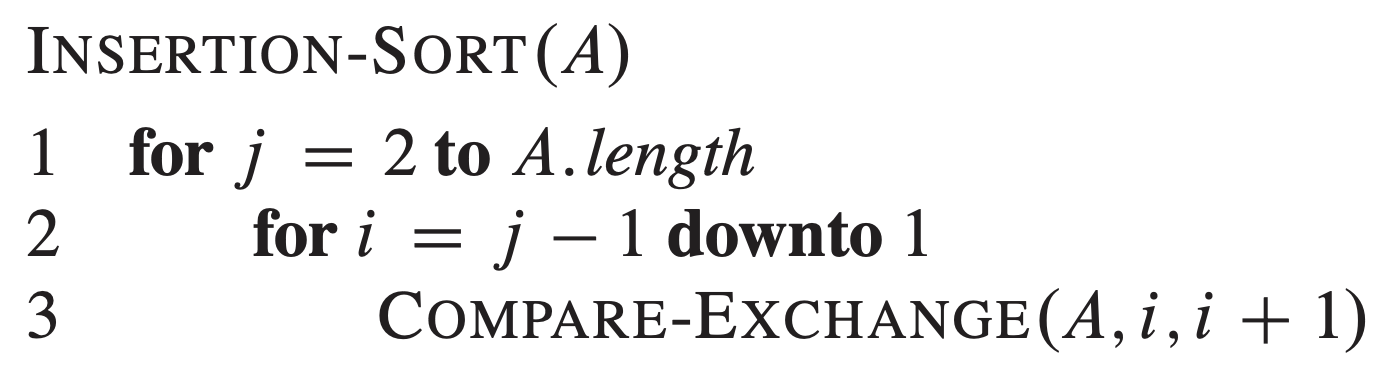
0-1 排序引理 提供了有力的方法来证明一个遗忘比较交换算法可以产生正确的排序结果。该引理表明，如果一个遗忘比较交换算法能够对所有只包含 $0$ 和 $1$ 的输入序列排序，那么它也可以对包含任意值的输入序列排序。

你可以通过其逆否命题来证明 0-1 排序引理：如果一个遗忘比较交换算法不能对某个包含任意值的序列进行排序，那么它也不能对某个 0-1序列进行排序。不妨假设一个遗忘比较交换算法 $X$ 未能对数组 $A[1..n]$ 排序。设 $A[p]$ 是算法 $X$ 未能将其放到正确位置的最小元素，而 $A[q]$ 是被算法 $X$ 放在 $A[p]$ 原本应该在的位置上的元素。定义一个只包含 $0$ 和 $1$ 的数组 $B[1..n]$ 如下：

$B[i] = \begin{cases}$
0 &\text{if } A[i] \le A[p] \
1 &\text{if } A[i] > A[p]\
\end{cases}

1. 讨论：$A[q] > A[p]$ 时，从而 $B[p] = 0$ 且 $B[q] = 1$ 。

2. 为了完成 0-1 排序引理的证明，请先证明算法 $X$ 不能对数组 $B$ 正确地排序。

现在，需要用 0-1 排序引理来证明一个特别的排序算法的正确性。 列排序 算法是用于包含 $n$ 个元素的矩形数组的排序。这一矩形数组有 $r$ 行 $s$ 列（因此 $n = rs$ ），满足下列三个限制条件：

• $r$ 必须是偶数；

• $s$ 必须是 $r$ 的因子；

• $r \ge 2s^2$ ；

当列排序完成时，矩形数组是 列优先有序 的：按照列从上到下，从左到右都是单调递增的。

如果不包括 $n$ 的值的计算，列排序需要 8 步操作。所有奇数步都一样：对每一列单独进行排序。每一个偶数步是一个特定的排列。具体如下：

• 第 1 步：对每一列进行排序。

• 第 2 步：转置这个矩形数组，并重新规整化为 $r$ 行 $s$ 列的形式。也就是说，首先将最左边的一列放在前 $r / s$ 行，然后将下一列放在第二个 $r / s$ 行，依此类推。

• 第 3 步：对每一列进行排序。

• 第 4 步：执行第 2 步排列操作的逆操作。

• 第 5 步：对每一列进行排序。

• 第 6 步：将每一列的上半部分移动到同一列的下半部分位置，将每一列的下半部分移到下一列的上半部分，并将最左边一列的上半部分置为空。此时，最后一列的下半部分成为新的最右列的上半部分，新的最右列的下半部分为空。

• 第 7 步：对每一列进行排序。

• 第 8 步：执行第 6 步排列操作的逆操作。

下图展示了一个在 $r=6$ 和 $s = 3$ 情况下的列排序步骤（即使这个例子违背了 $r \ge 2s^2$ 的条件，列排序仍然有效）。

3. 讨论：即使不知道奇数步采用了什么排序算法，我们也可以把列排序看做一种遗忘比较算法。

虽然似乎很难让人相信列排序也能实现排序，但是你可以利用 0-1 排序引理来证明这一点。因为列排序可以看做是一种遗忘比较交换算法，所以我们可以使用 0-1 排序引理。下面一些定义有助于你使用这一引理。如果数组中某个区域只包含全 0 或者全 1 ，我们定义这个区域是 干净的 。否则，如果这个区域包含的是 0 和 1 的混合，则称这个区域是 脏的 。这里，假设输入数据只包含 0 和 1 ，且输入数据能够被转换为 $r$ 行 $s$ 列。

4. 证明：经过第 1 到 3 步，数组由三部分组成：顶部一些由全 0 组成的干净行，底部一些由全 1 组成的干净行，以及中间最多 $s$ 行脏的行。

5. 证明：经过第 4 步之后，如果按照列优先原则读取数组，先读到的是全 0 的干净区域，最后是全 1 的干净区域，中间是由最多 $s^2$ 个元素组成的脏的区域。

6. 证明：第 5 到 8 步产生一个全排序的 0-1 输出，并得到结论：列排序可以正确地对任意输入值排序。

Solution

1. 因为 $A[p] \le A[p]$ 是显然的，所以 $B[p] = 0$ 。由于 $A[p]$ 是被放错位置的最小的元素，所以 $A[q] > A[p]$ （因为最小，所以 $A[q] \ge A[p]$ ，因为放错，所以 $A[q] \ne A[p]$），从而 $B[q] = 1$ 。

2. 令 $A_i, B_i$ 分别是 $A, B$ 在被 $X$ 进行 $i$ 次遗忘比较交换操作后的结果，显然 $A = A_0, B = B_0$ 。下面用数学归纳法证明：

$\forall i, j, A_i[j] > A[p] \Leftrightarrow B_i[j] > B[p]$

• 基础情况： $i = 0$ 时，根据 $B[i]$ 的定义，结论显然正确。

• 归纳假设： 假设前 $i$ 次遗忘比较操作后，结论依然成立。

• 归纳步骤： 进行第 $i + 1$ 次遗忘比较操作后，假设其作用在位置 $j_1$ 和位置 $j_2$ 上，其中 $j_1 < j_2$ 。根据归纳假设，不可能有 $A_i[j_1] \le A_i[j_2]$ 且 $B_i[j_1] > B_i[j_2]$ ，因为 $B_i[j_1] > B_i[j_2]$ 意味着 $A_i[j_1] > A[p] \ge A_i[j_2]$ ，矛盾。于是我们只剩 3 种可能的情况：

  • 情况1： $A_i[j_1] \le A_i[j_2]$ 且 $B_i[j_1] \le B_i[j_2]$ 。第 $i + 1$ 次操作不会产生交换，即 $A_{i+1} = A_{i}, B_{i+1} = B_{i}$ ，结论显然成立。

  • 情况2： $A_i[j_1] > A_i[j_2]$ 且 $B_i[j_1] \le B_i[j_2]$ 。第 $i + 1$ 次操作会在 $A$ 中产生交换，但不会在 $B$ 中产生交换。我们也清楚，$A_i[j_1]$ 和 $A_i[j_2]$ 都大于 $A[p]$ ，要么都小于等于 $A[p]$ 。否则我们会有 $B_i[j_1] \ne B_i[j_2]$ ，从而 $0 = B_i[j_1] < B_i[j_2] = 1$ ，这意味着 $A_i[j_1] \le A[p] < A_i[j_2]$ ，和情况 2 矛盾。第 $i + 1$ 次交换都比 $A[p]$ 大或者都不超过 $A[p]$ 的两个元素 $A_i[j_1]$ 和 $A_i[j_2]$ 并不会影响它们和 $A[p]$ 的大小关系，因此也就不会破坏结论，结论依旧成立。

  • 情况3： $A_i[j_1] > A_i[j_2]$ 且 $B_i[j_1] > B_i[j_2]$ 。第 $i + 1$ 次操作会在 $A$ 和 $B$ 中都产生一次交换。由于原本有 $A_i[j_1] > A[p] \Leftrightarrow B_i[j_1] > 0$ ，两个数组中都发生交换后有 $A_{i+1}[j_2] > A[p] \Leftrightarrow B_{i+1}[j_2] > 0$ ，对于 $j_1$ 也是类似的成立。除了 $j_1, j_2$ 以外的位置均未发生改变，因此结论依旧成立。

• 综上，$\forall i, j, A_i[j] > A[p] \Leftrightarrow B_i[j] > B[p]$ 。

令 $i$ 为 $X$ 算法中总的遗忘比较交换操作次数， $j$ 为最终 $A[p]$ 的位置， $k$ 是 $A[p]$ 应该在的位置。我们知道 $k < j$ ，因为 $A[p]$ 是最小的没有被正确排序的元素。根据定义， $A[q] = A_i[k], A[p] = A_i[j]$ ，从第 1 问中，我们知道 $A_i[k] > A_i[j] = A[p]$ 。根据上面证明的结论，有 $B_i[k] > B[p] = 0 = B_i[j]$ ，因此 $(k, j)$ 是一个逆序对， $X$ 算法并没有对数组 $B$ 正确地排序。

3. 算法中所有的偶数步其实根本就没有看具体元素的值，只是以固定地方式挪动位置，因此既不依赖待排序元素的值，也不依赖之前的比较结果。由于奇数步中的排序没有作任何方法上的限制，因此也可以认为符合遗忘比较交换算法的条件。因此，列排序的奇数步和偶数步都符合遗忘比较交换算法的条件，列排序是一个遗忘比较交换算法。

4. 在第 1 步之后，每一列都应当是一些 0 之后紧跟一些 1 的形式，假设第 $i$ 列中有 $z_i$ 个 0 。那么，在第二步转置并规整化之后，之前的每一列应当贡献 $\lceil z_i / s \rceil$ 个 0 到之后的前 $z_i \bmod s$ 列，而对剩余列贡献少一个。也就是说，之前的每一列对于现在的每一列要么贡献 $\lceil z_i / s \rceil$ 个 0 ，要么贡献 $\lceil z_i / s \rceil - 1$ 个 0 ，从而现在每一列的 0 的个数 $z&#x27;_i$ 的范围是

$\sum_{i=1}^{s} (\lceil z_i / s \rceil - 1) \le z&#x27;$i \le \sum{i=1}^{s} \lceil z_i / s \rceil

这个范围区间的大小为 $s$ ，也就意味着第 3 步排序后最多有 $s$ 行的脏行。

5. 根据第 4 问，中间最多有 $s$ 行脏行，意味着最多 $s^2$ 个脏元素。第 4 步会讲原本的行映射成列，按照第 4 步结果列优先读取数据和按照第 3 问结果行优先读取数据得到的效果是等价的，都是先全 0 ，再最多 $s^2$ 的脏的区域，最后全 1 。

6. 从第 5 问中我们知道，第 4 步之后最多有中间 $s^2$ 个元素是没有排好序的脏的区域。而 $r >= 2s^2$ ，则有两种情况：

   • 第 1 种情况，脏区域横跨两列，那么在第 6 步之后，脏区域就只在一列之中，第 7 步排序可以消除脏区域，从而整个矩形数组列优先排序已完成，后续的步骤并不会破坏这种排序性质。

   • 第 2 种情况，脏区域在一列之中，那么在第 5 步就已经将这一列排好序了，后续步骤并不会破坏这种排序性质。

   • 综上，列排序算法是正确的。