Problem 1 (教材习题 8.1-1)

在一棵比较排序算法的决策树中，一个叶结点可能的最小深度是多少？

Solution

为了得到 $a_1 \le a_2 \le \cdots \le a_n$ 的比较结果，我们至少需要 $n - 1$ 次比较，并且这 $n - 1$ 次比较能够恰好串成一个形如 $a_1 \le a_2 \le \cdots \le a_n$ 的不等式链。因此，一个叶结点可能的最小深度为 $n - 1$ 。

Problem 2 (教材习题 8.1-2)

不用斯特林公式，给出 $\log n!$ 的渐进紧确界。利用作业6-1问题3第4问中涉及的技术来求累加和 $\sum\limits_{k=1}^{n} \log k$ 。

Solution

直接放缩求上界：

$\log n! = \sum_{k=1}^{n} \log k \le \sum_{k=1}^{n} \log n = n\log n$

折半放缩求下界：

$\begin{aligned}$
\log n! &= \sum_{k=1}^{n} \log k\
&= \sum_{k=1}^{n/2} \log k + \sum_{k=n/2 + 1}^{n} \log k\
&\ge \sum_{k=1}^{n/2} 1 + \sum_{k=n/2 + 1}^{n} \log(n/2)\
&= \frac{n}{2} + \frac{n}{2}(\log n - 1)\
&= \frac{n}{2}\log n
\end{aligned}

综上， $\frac{1}{2} n\log n \le \log n! \le n\log n$ ，所以 $\log n! = \Theta(n\log n)$ 。

Problem 3 (教材习题 8.1-3)

证明：对于 $n!$ 种长度为 $n$ 的输入中的至少一半，不存在能达到线性运行时间的比较算法。如果只要求对 $1/n$ 的输入达到线性时间呢？$1 / 2^n$ 呢？

Solution

证明：作最保守的估计，假设决策树只有 $n! / 2$ 个叶子，即只能对于其中 $n!/2$ 种输入排序，剩余的输入情况直接不考虑。如果在这种假设下还不能够达到线性时间，那么无论如何也不能够达到线性时间了。

考虑其树的高度为 $h$ ，它最多有 $2 ^ h$ 个叶子，从而

$2^h \ge \frac{n!}{2} \Rightarrow h \ge \log\frac{n!}{2} = \log n! - 2 = \Theta(n \log n) = \omega(n)$

因此，不可能存在线性时间的算法。

类似的，对于 $1/n$ 的输入：

$2^h \ge \frac{n!}{n} \Rightarrow h \ge \log\frac{n!}{n} = \log n! - \log n = \Theta(n \log n) = \omega(n)$

$2^h \ge \frac{n!}{2^n} \Rightarrow h \ge \log\frac{n!}{2^n} = \log n! - n = \Theta(n \log n) = \omega(n)$

都不可能达到线性复杂度。

其实这道题想说的就是 $n!$ 增长的超级快，即使你只需要其中的 $1 /2^n$ 种情况能拍好序，也必须要 $\Omega(n\log n)$ 的时间才行。

Problem 4 (教材习题 8.1-4)

假设现在有一个包含 $n$ 个元素的待排序序列。该序列由 $n / k$ 个子序列组成，每个子序列包含 $k$ 个元素。一个给定子序列中的每个元素都小于其后继子序列中的所有元素，且大于其前驱子序列中的每个元素。因此，这个长度为 $n$ 的序列的排序转化为对 $n / k$ 个子序列中的 $k$ 个元素的排序。试证明：这个排序问题中所需比较次数的下界是 $\Omega(n\log k)$ 。（提示：简单地将每个子序列的下界进行合并是不严谨的。）

Solution

证明：考虑这个排序问题的任意算法的决策树，这个序列有 $(k!)^{n/k}$ 种可能的排列情况，也就是说如果算法能够正确地排序，那么它对应的决策树至少有 $(k!)^{n/k}$ 个叶子结点。记其高度为 $h$ ，则最多有 $2^h$ 个叶子结点，于是我们有

$2^h \ge (k!)^{n/k} \Rightarrow h \ge \frac{n}{k} \log (k!) = \frac{n}{k} \Theta(k\log k) = \Theta(n\log k)$

从而， $h = \Omega(n\log k)$ 。

Problem 5 (教材习题 8.2-2)

试证明 COUNTING-SORT （详见第7讲PPT第11页）是稳定的（详见第7讲PPT第15页）。

Solution

证明：考虑任意的 $A[i] = A[j] = k$ ，其中 $i < j$ 。

下面证明 COUNTING-SORT 运行结束后， $A[i]$ 和 $A[j]$ 所对应的 $B[i&#x27;]$ 和 $B[j&#x27;]$ 依旧满足 $i&#x27; < j&#x27;$ 。

考虑算法第 10 到 12 行的 for 循环，在这个循环中，我们借助计数数组 $C$ ，利用输入数组 $A$ 中的元素构造了输出数组 $B$ 。

由于 $j > i$ ，循环会先处理 $A[j]$ ，后处理 $A[i]$ 。不妨设 $C[k] = m$ ，则算法第 11 行会将 $B[m]$ 赋值为 $A[j]$ ，即 $j&#x27; = m$ 。

之后算法第 12 行会将 $C[k]$ 赋值为 $m - 1$ ，并且循环只会减少 $C$ 中的值，因此后续迭代中 $A[i]$ 的时候，必然有 $C[k] \le m - 1$ ，从而 $i&#x27; \le m - 1 < m = j&#x27;$ 。

综上， $i&#x27; < j&#x27;$ 得证， COUNTING-SORT 是稳定的。

Problem 6 (教材习题 8.2-3)

假设我们在 COUNTING-SORT （详见第7讲PPT第11页）的第 10 行循环的开始部分，将代码改写为

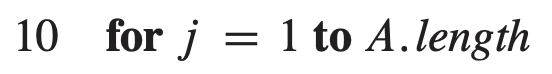
试证明该算法仍然是正确的。它还稳定吗？

Solution

证明：算法依旧正确。算法第 11 到 12 行从 $C$ 中取出下标，把对应 $A$ 中元素放入 $B$ 中对应位置，这个过程中是根据 $A$ 中元素从后往前的顺序进行还是从前往后的顺序进行并不会影响同一样大小的元素在结果数组 $B$ 中的整体位置。

具体地，大小为 $k$ 的元素，依旧会放置在 $B[C[k-1] + 1 .. C[k]]$ 这个区间中。只不过这个时候，同样大小为 $k$ 的元素，在 $A$ 中靠前的会被放到 $B[C[k-1] + 1 .. C[k]]$ 靠后的位置上，也就是稳定性被破坏了，并且在一个“值区间”内，输入数组和输出数组中等值元素的顺序是刚好相反的。

Problem 7 (教材习题 8.2-4)

设计一个算法，它能够对于任何给定的介于 $0$ 到 $k$ 之间的 $n$ 个整数先进行预处理，然后在 $O(1)$ 时间内回答输入的 $n$ 个整数中有多少个落在区间 $[a..b]$ 内。你设计的算法与处理时间应为 $\Theta(n + k)$ 。

Solution

预先处理阶段和 COUNTING-SORT （详见第7讲PPT第11页） 算法的第 1 到 9 行完全相同，这样的话 $C[i]$ 就包含了小于等于 $i$ 的元素个数。

要求 $[a..b]$ 内的元素个数的话，只需要计算 $C[b] - C[a-1]$ 即可。