Problem 1 (教材习题 9.3-3)

假设所有元素都是互异的，说明在最坏情况下，如何才能使快速排序的运行时间为 $O(n\log n)$ ？

Solution

由于我们已经可以通过 BFPRT 的 SELECT 算法（详见第8讲PPT第14页）在每次 PARTITION 的时候手动地在线性时间内选择中位数作为主元，从而快速排序的递归式变为

$T(n) = 2T(n / 2) + O(n)$

不难得到，$T(n) = O(n\log n)$ ，快速排序的最坏情况运行时间也被改进到了 $O(n\log n)$ ，只不过这里面蕴含的常数系数会很大。

Problem 2 (教材习题 9.3-4)

对一个包含 $n$ 个元素的集合，假设一个算法只使用比较来确定第 $i$ 小的元素，证明：无需额外的比较操作，它也能找到前 $i - 1$ 小的元素和前 $n - i$ 大的元素。

Solution

证明：构建一个有 $n$ 个结点 ${1, 2, \cdots ,n}$ 的有向图，如果在该算法运行过程中比较了 $A[i]$ 和 $A[j]$ ，并且得出结论 $A[i] \ge A[j]$ ，则有一条从结点 $i$ 到结点 $j$ 的有向边。从而，整张图中的有向边表示了该算法过程中发现的所有的大于等于关系。

假设第 $i$ 大的元素为 $A[x]$ ，观察到， $A[i]$ 是前 $i - 1$ 小的元素之一当且仅当图中存在一条从 $x$ 到 $i$ 的路径； $A[i]$ 是前 $n - i$ 大的元素之一当且仅当图中存在一条从 $i$ 到 $x$ 的路径。

图中的每个结点 $i$ 都必须在一条从 $x$ 出发的或者走向 $x$ 的路径上面，否则算法就无法区分 $A[i] \le A[x]$ 和 $A[i] \ge A[x]$ 。此外，如果既存在从 $x$ 到 $i$ 的路径，也存在从 $i$ 到 $x$ 的路径，说明 $A[x] \ge A[i] \wedge A[i] \ge A[x]$ ，即 $A[i] = A[x]$ ，我们可以任意地区分相等的元素是前 $i - 1$ 小还是前 $n - i$ 大。

综上，我们可以判断所有的结点到底是前 $i - 1$ 小的元素还是前 $n - i$ 大的元素，且无需额外的比较操作。

Problem 3 (教材习题 9.3-6)

对一个包含 $n$ 个元素的集合来说， $k$ 分位数 是指能把有序集合分成 $k$ 个等大集合的 $k - 1$ 个顺序统计量。给出一个能找出某一集合的 $k$ 分位数的 $O(n\log k)$ 时间的算法。

Solution

不失一般性，假设 $n$ 和 $k$ 都是 $2$ 的幂次。首先使用 SELECT 算法在 $O(n)$ 时间内寻找第 $n/2$ 个顺序统计量 ，利用该顺序统计量，我们将原问题划分为两个子问题：我们只需要分别在前 $n/2$ 和后 $n/2$ 个元素中寻找其 $k/2$ 分位数即可。该算法的递归式为

$T(n, k) = \begin{cases}$
O(1) & \text{if } k = 1\
2T(n/2, k/2) + O(n) & \text{if }k > 1
\end{cases}

代入 $O(n) \le cn$ ，解该递归式，有

$\begin{aligned}$
T(n, k) &\le cn + 2T(n/2, k/2)\
&\le 2cn + 4T(n/4, k/4)\
&\le 3cn + 8T(n/8, k/8)\
&\vdots\
&\le (\log k) \cdot cn + k T(n/k, 1)
&=(\log k) \cdot cn + k \cdot O(1)\
&=O(n\log k)
\end{aligned}

于是，该算法的复杂度为 $O(n\log k)$ 。其实这就是一个朴素二分的分治算法。

Problem 4 (教材习题 9.3-7)

设计一个 $O(n)$ 时间的算法，对于一个给定的包含 $n$ 个互异元素的集合 $S$ 和一个正整数 $k \le n$ ，该算法能够确定 $S$ 中最接近中位数的 $k$ 个元素。

Solution

先用 $O(n)$ 的时间找到中位数。创建一个新的数组，其中每个元素是原本元素减去中位数的绝对值，需要 $O(n)$ 时间。寻找这个新数组中的前 $k$ 小元素，需要 $O(n)$ 时间。原来数组中最接近中位数的 $k$ 个元素就是和中位数作差后绝对值前 $k$ 小的元素。上述算法整体复杂度为 $O(n)$ 。

Problem 5 (教材习题 9.3-8)

设 $X[1..n]$ 和 $Y[1..n]$ 为两个数组，每个都包含 $n$ 个有序的元素。请设计一个 $O(\log n)$ 时间的算法来找出数组 $X$ 和 $Y$ 中所有 $2n$ 个元素的中位数。

Solution

不失一般性，假设 $n$ 是 $2$ 的幂次。

记算法的运行时间为 $T(n)$ ，不难看出 $T(n) = T(n/2) + O(1)$ ，则 $T(n) = O(\log n)$ 。

Problem 6 (教材习题 9.3-9)

熊教授是一家石油公司的顾问。这家公司正在计划建造一条从东向西的大型输油管道，这一管道将穿越一个有 $n$ 口油井的油田。公司希望有一条管道支线沿着最短路径从每口油井连接到主管道（方向或南或北），如下图所示。

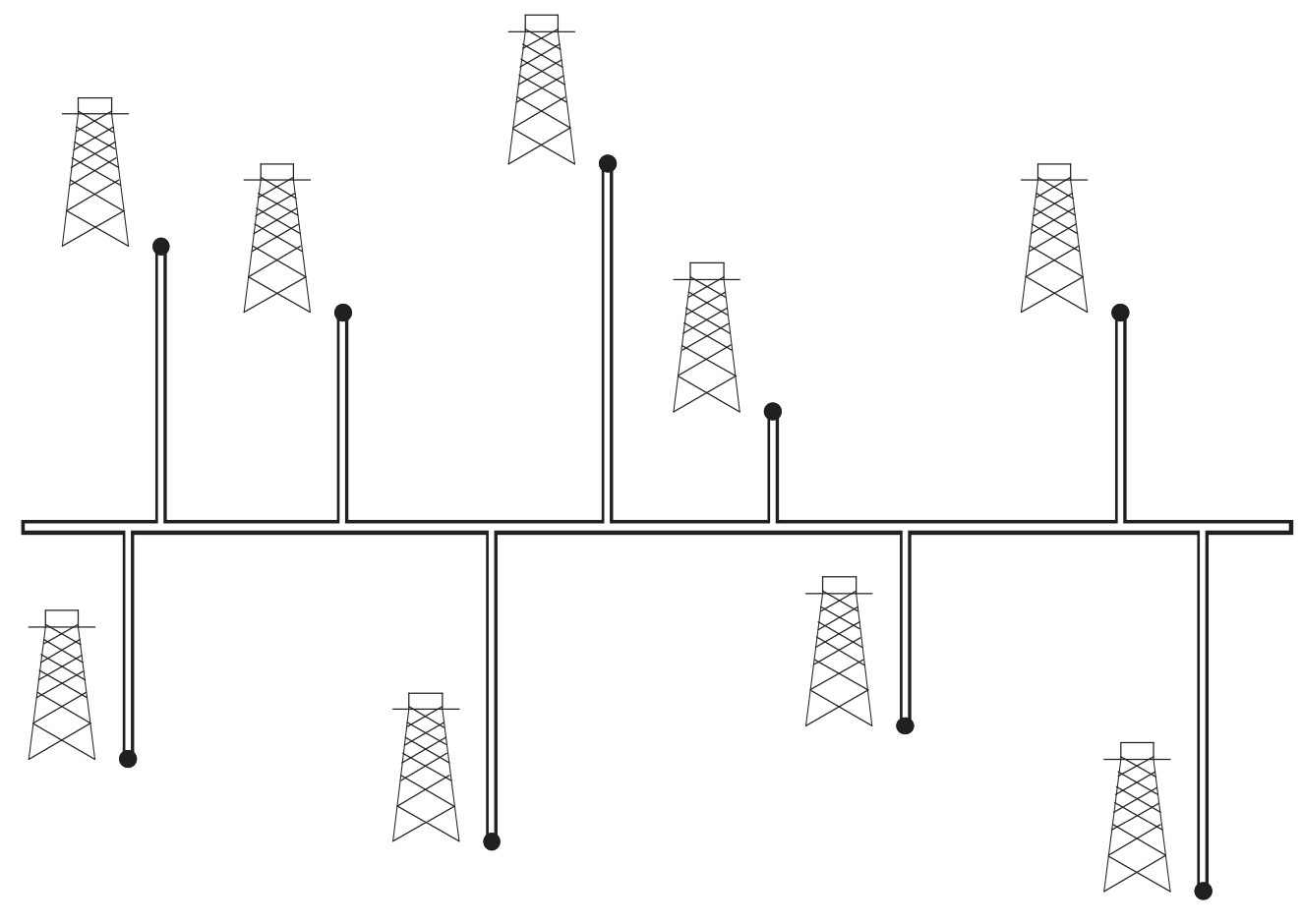
给定每口油井的 $x$ 和 $y$ 坐标，教授应该如何选择主管道的最优位置，使得各直线的总长度最小？证明：该最优位置可以在线性时间内确定。

Solution

首先，东西方向的主管道长度是固定的，就是 $x$ 的最大值减去 $x$ 的最小值，这是可以在线性时间内确定的，并且和主管道的位置无关。

下面，我们只需要考虑如何选择主管道的位置，使得各个南北方向的连接管道长度之和最短即可。

假设 $y_1, y_2,\cdots,y_n$ 是所有油田的纵坐标， $y$ 是主管道的位置，则所有南北方向的连接管道的长度之和 $f(y)$ 为

$f(y) = \sum_{i=1}^{n} |y - y_i|$

不难看出 $f(y)$ 是一个先减后增的连续函数。

• 当 $n$ 为奇数时， $f(y)$ 在 $y$ 取 $y_1, y_2,\cdots,y_n$ 的中位数时取到最小值，求中位数只需线性时间。

• 当 $n$ 为偶数时， $f(y)$ 在 $y$ 等于 $y_1, y_2,\cdots,y_n$ 的上下中位数之间的任何值（含上下中位数）的时候取到最小值，求上下中位数只需线性时间。

综上，如果有奇数个油田就取纵坐标的中位数位置建主管道，偶数个油田就取纵坐标上下中位数之间（含上下中位数）的任意位置建主管道。主管道的东西端点取所有油田横坐标的最小值和最大值即可。这些都可以在线性时间内确定。